Question

2-55 Nite Time Inn has a toll-free telephone number so that customers can call at any time to make a reservation. A typical call takes about 4 minutes to complete, and the time required follows an exponential distribution. Find the probability that a call takes

Answer 1

The question is incomplete. Here is the complete question.

Nite Time Inn has a toll-free telephone number so that customers can call at any time to make a reservation. A typical call takes about 4 minutes to complete, and the time required follows an exponential distribution. find the probability that a call takes

a) 3 minutes or less

b) 4 minutes of less

c) 5 minutes of less

d) Longer than 5 minutes

e) Longer than 7 minutes

Answer: a) P(X<3) = 0.882

b) P(X<4) = 0.908

c) P(X<5) = 0.928

d) P(X>5) = 0.286

e) P(X>7) = 0.174

Explanation: Exponential distribution is related with teh amount of time until some specific event happens.

If X is a continuous random variable, probability is calculated as:

`P(X<x) = 1-me^(-mx)`

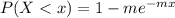
in which:

m is decay parameter, given by:
`m=(1)/(mean)`

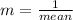
For the Nite Time Inn calls:

`m=(1)/(4)`

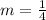
m = 0.25

(a) P(X<3)

`P(X<3) = 1-0.25e^(-0.25.3)`

`P(X<3) = 1-0.25e^(-0.75)`

`P(X<3) = 1-0.25*0.472`

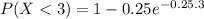
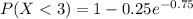
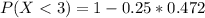
P(X < 3) = 0.882

The probability the call takes less than 3 minutes is 0.882.

(b) P(X<4)

`P(X<4) = 1-0.25e^(-0.25.4)`

`P(X<4) = 1-0.25e^(-1)`

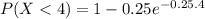
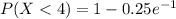
P(X < 4) = 0.908

The probability the call takes less tahn 4 minutes is 0.908.

(c) P(X<5)

`P(X<5) = 1-0.25e^(-0.25.5)`

`P(X<5) = 1-0.25e^(-1.25)`

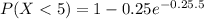
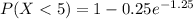
P(X < 5) = 0.928

The probability of calls taking less than 5 minutes is 0.928.

(d) P(X>5)

Knowing that the sum of probabilities of less than and more than has to equal 1:

P(X<x) + P(X>x) = 1

P(X>x) = 1 - P(PX<x)

`P(X>x) = 1-(1-me^(-m*x))`

`P(X>x)=me^(-mx)`

For P(X>5):

`P(X>5) = 0.25e^(-1.25)`

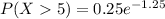
P(X > 5) = 0.286

The probability of calls taking more than 5 minutes is 0.286.

(e) P(X>7)

`P(X>7)=0.25e^(-0.25.7)`

`P(X>7)=0.25e^(-1.75)`

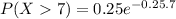
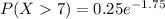
P(X > 7) = 0.174

The probability of calls taking more than 7 minutes is 0.174.