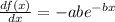Question

What is the first derivative of the following function: f(x) = aexp(-bx)

Answer 1

The first derivative of the given function

`(df(x))/(dx) = - ab e^(-b x)`

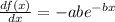
Explanation:

Step(i):-

Given f(x) = ae⁻ᵇˣ ...( i )

we will use differentiation formula

`(d(e^(ax)) )/(dx) = a e^(a x)`

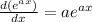
Step(ii)

Differentiating equation (i) with respective to 'x', we get

`(df(x))/(dx) = a e^(-b x) (d)/(dx) (-b x )`

= -ab e⁻ᵇˣ

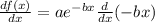
`(df(x))/(dx) = - ab e^(-b x)`

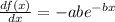
Final answer:-

The first derivative of the given function

`(df(x))/(dx) = - ab e^(-b x)`