Question

If the endpoints of segment AB are A(-4,5) and B(2,-5),

please help! ​

Answer 1

`d = \sqrt[2]{34}`

Explanation:

We are solving for the segment of AB. Note that it is a line segment, so there will be end points, those being A(-4, 5) & B(2, -5).

Use the following distance formula:

`distance`
`(d) =`
`\sqrt{(x_(2) - x_(1))^(2) + (y_(2) - x_(2))^2 }`

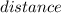
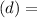
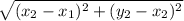
Let:

Point B(2 , -5) = (x₁ , y₁)

Point A(-4 , 5) = (x₂ , y₂)

Plug in the corresponding numbers to the corresponding variables.

`d =`
`\sqrt{(-4 - 2)^(2) + (5 - (-5))^(2) }`

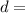
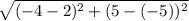
Simplify. Remember to follow PEMDAS. First, solve the parenthesis, then the powers, then add, and then finally square root.

`d = \sqrt{(-6)^(2) + (5 + 5)^(2) } \\d = √((-6 * -6) + (10)^2) \\d = √((36) + (10 * 10)) \\d = √(36 + (100)) \\d = √(136)`

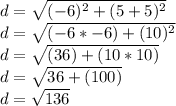
Simplify:

`d = √(136) = √(2 * 2 * 2 * 17) = \sqrt[2]{17 * 2} = \sqrt[2]{34}`

`d = \sqrt[2]{34}` is your answer.

~