Question

Suppose we are estimating a population proportion by its sample equivalent.

(a) We have a sample of n = 10 units and we find the proportion is p = .4. If the true proportion is p= .3 find PC Ô-p|>.2)
(b) Consider the same problem as in part (a) but now, our sample size is n = 400. Find P( P-p> .001)

Answer 1

(a) 0.16759

(b) 0.9649

Explanation:

Given that:

n = 10 , p = 0.3 and
`\hat p = 0.4`

`P(|\hat p - p| > 0.2 ) = 1 - P ( |\hat p -p| \leq 0.2)`

=
`1 - P(-0.2 \leq \hat p-p \leq 0.2)`

=
`1 - P \begin {pmatrix} \frac{-0.2}{\sqrt{(pq)/(n)}} \leq \frac{\hat p -p}{\sqrt{(pq)/(n)}} \leq \frac{0.2}{\sqrt{(pq)/(n)}} \end {pmatrix}`

`=1 - P \begin {pmatrix} \frac{-0.2}{\sqrt{((0.3)(1-0.3))/(10)}} \leq Z \leq \frac{0.2}{\sqrt{((0.3)(1-0.3))/(10)}} \end {pmatrix}`

`=1 - P \begin {pmatrix} \frac{-0.2}{\sqrt{((0.3)(0.7))/(10)}} \leq Z \leq \frac{0.2}{\sqrt{((0.3)(0.7))/(10)}} \end {pmatrix}`

`=1 - P \begin {pmatrix} (-0.2)/(√(0.021)) \leq Z \leq (0.2)/(√(0.021)) \end {pmatrix}`

`=1 - P \begin {pmatrix} -1.380 \leq Z \leq 1.380 \end {pmatrix}`

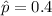
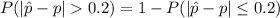
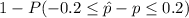
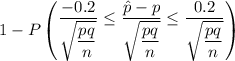
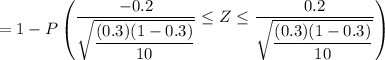
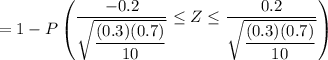
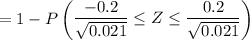
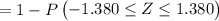
= 1 - P( Z ≤ 1.380) - P(-1.380)

= 1 - ( 0.91620 - 0.08379 )

= 1 - 0.83241

= 0.16759

b) when n = 400; p =0.3 , q = 1 - p = 1 - 0.3 = 0.7

`P( |\hat p - p | > 0.001) = 1- P ( |\hat p - p | < 0.001 )`

`= 1- P ( -0.001 < \hat p - p < 0.001 )`

`= 1- P ( \frac{-0.001}{\sqrt{(pq)/(n)}} < ( \hat p - p)/((pq)/(n)) < \frac{0.001}{\sqrt{(pq)/(n)}} )`

`= 1- P ( \frac{-0.001}{\sqrt{(0.3* 0.7)/(400)}} < Z < \frac{0.001}{\sqrt{(0.3 * 0.7)/(400)}} )`

`= 1- P ( \frac{-0.001}{\sqrt{5.25 * 10^(-4)}} < Z < \frac{0.001}{\sqrt{5.25 * 10^(-4)}} )`

`= 1- P ( -0.0436< Z < 0.0436)`

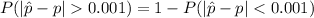
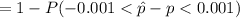
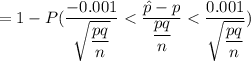
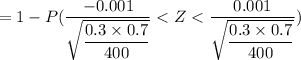
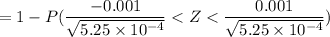
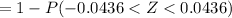
= 1 - P ( Z < 0.0436) - P ( -0.0436)

= 1 - (0.5176 - 0.4825)

= 1 - 0.0351

= 0.9649