Answer:
A) The distance between the stations is 1430m
B) The time it takes the train to go between the stations is 80s
Step-by-step explanation:
First we will calculate the distance covered for the first 20s.
From one the equations of kinematics for linear motion
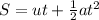
Where
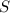 is distance traveled
is distance traveled
 is the initial velocity
is the initial velocity
 is time
is time
and
 is acceleration
is acceleration
Since the train starts from rest,
 = 0 m/s
= 0 m/s
Hence, for the first 20s
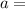 1.1 m/s²;
1.1 m/s²;
 20s,
20s,
 = 0 m/s
= 0 m/s
∴
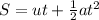 gives
gives

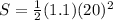
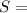 220m
220m
This is the distance covered in the first 20s.
- The train then proceeds at constant speed for 1100m.
Now, we will calculate the speed attained here
From
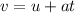
Where
 is the final velocity
is the final velocity
Hence,

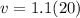
 22 m/s
22 m/s
This is the constant speed attained when it proceeds for 1100m
- The train then slows down at a rate of 2.2 m/s² until it stops
We can calculate the distance covered while slowing down from

The initial velocity,
 here will be the final velocity before it started slowing down
here will be the final velocity before it started slowing down
∴
 = 22 m/s
= 22 m/s
The final velocity will be 0, since it came to a stop.
∴
 = 0 m/s
= 0 m/s
 2.2 m/s² ( - indicates deceleration)
2.2 m/s² ( - indicates deceleration)
Hence,
 gives
gives
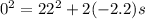

This is the distance traveled while slowing down.
A) The distance between the stations is
220m + 1100m + 110m
= 1430m
Hence, the distance between the stations is 1430m
B) The time it takes the train to go between the stations
The time spent while accelerating at 1.1 m/s² is 20s
We will calculate the time spent when it proceeds at a constant speed of 22 m/s for 1100m,
From,
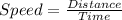
Then,
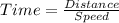
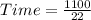
Time = 50 s
And then, the time spent while decelerating (that is, while slowing down)
From,
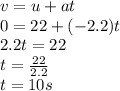
This is the time spent while slowing down until it stops at the station.
Hence, The time it takes the train to go between the stations is
20s + 50s + 10s = 80s
The time it takes the train to go between the stations is 80s