Answer:
reject the null hypothesis
Explanation:
Total observation = 27+49+24 = 100
Expected Frequency :
Half Pint = 100 × 0.4 = 40
XXX = 100 × 0.4 = 40
Dark night = 100 × 0.2 = 20
The Chi-square goodness-of-fit test can be computed as follows:
Observed Expected
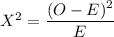
Frequency(O) Frequency (E)
Half- 27 40 4.225
Pint
XXX 29 40 3.025
Dark- 24 20 0.8
night
Total 100 100 8.05
The test statistics
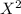 = 8.05
= 8.05
8.05
degree of freedom = n -1
degree of freedom = 3 - 1
degree of freedom = 2
The p-value can be computed by using the EXCEL FORMULA (=CHIDIST(8.05,2)
p-value = 0.01786
Since the p-value is less than the level of significance, we reject the null hypothesis
Also using the critical value approach from the EXCEL FUNCTION;
critical chi-square (=CHIINV(0.05,2) = 5.99
 , therefore, we reject the null hypothesis
, therefore, we reject the null hypothesis