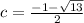Answer:
a)
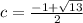 and
and
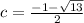
Explanation:
The idea for the solution of this equation is to find the value of c where both parts of the piecewise-defined function are the same. So we need to take the parts of the function and set them equal to each other, so we get:
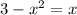
and then solve for x. We move everything to one side of the equation so we get:
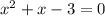
and we use the quadratic formula:
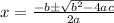
and we substitute:
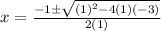
and solve
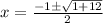
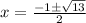
so our two answers are:
a)
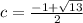 and
and