Question

A scientist needs 10 liters of a 20% acid solution for an experiment, but she has only a 5% solution and a 40% solution. To the nearest tenth of a liter, about how many liters of the 5% and the 40% solutions should she mix to get the solution she needs? Choose the equation to match the situation

Answer 1

The volume of 40% solution= 4.3L

The volume of 5% solution= 10L - 4.3L= 5.7L

Explanation:

From the given information:

Let consider x to be the of volume 40% solution

therefore the volume of 5% is said to be:

10 L= 40% solution volume + 5% solution volume

10 L= (x + 5%) solution volume

making 5% solution volume the subject; we have

5% solution volume= 10 L - x

To estimate the value of the volume, we now have:

Volume of 20% × Concentration of 20%= (Volume of 40% × concentration40%) + (Volume of 5% × Concentration of 5% )

∴

10L × 20%= (x) L × 35% + 10 L × 5%

(x) L × 35 = 10L × 20 - 10 L × 5 = 10 L × 15

`x L = 10L * (15)/(35)`

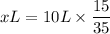
x = 4.28 L

x
`\simeq` 4.3L

∴

The volume of 40% solution= 4.3L

The volume of 5% solution= 10L - 4.3L= 5.7L