AB lies on a number line. The coordinate of point A is -6. Given that AB=20, what are two possible coordinates for point B?

Question

asked Oct 23, 2021 175k views

1 Answer

Jens Roland · Answer 1 · 2021-10-27T07:17:35+0000

Answer:

-26 or 14

Explanation:

Given that

Coordinate of point A is -6.

Length of AB = 20

To find:

Coordinates for the point B = ?

Solution:

We are given that:

AB = 20

In other words, we can use modulus function to define the distance between A and B:

|Coordinates of B - Coordinates of A| = 20

Let the coordinates of B =

Kindly refer to the attached image for the given situation.

Point B might be either on the left or on the right side of A.

That means:

$|x-(-6)| = 20\\\Rightarrow |x+6|=20$

Now, let us have a look at the modulus function:

$|y|=\left \{ {-{y}\ if\ y<0 \atop {y}\ if\ y>0} \right.$

So,

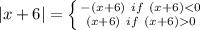
$|x+6|=\left \{ {-{(x+6)}\ if\ (x+6)<0 \atop {(x+6)}\ if\ (x+6)>0} \right.$

$(x+6 ) =20\\\Rightarrow x =14$

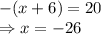
$-(x+6 ) =20\\\Rightarrow x =-26$

Therefore, the answer is:

-26 or 14