Question

A spherical balloon with a diameter of 9 m is filled with helium at 20°C and 200 kPa. Determine the mole number and the mass of the helium in the balloon.

Answer 1

number of mole is 31342.36 moles

mass is 125.369 kg

Step-by-step explanation:

Diameter of the spherical balloon d = 9 m

radius r = d/2 = 9/2 = 4.5 m

The volume pf the sphere balloon ca be calculated from

V =
`(4)/(3) \pi r^3`

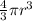
V =
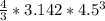`(4)/(3)* 3.142* 4.5^3` = 381.75 m^3

Temperature of the gas T = 20 °C = 20 + 273 = 293 K

Pressure of the helium gas = 200 kPa = 200 x 10^3 Pa

number of moles n = ?

Using

PV = nRT

where

P is the pressure of the gas

V is the volume of the gas

n is the mole number of the gas

R is the gas constant = 8.314 m^3⋅Pa⋅K^−1⋅mol^−1

T is the temperature of the gas (must be converted to kelvin K)

substituting values, we have

200 x 10^3 x 381.75 = n x 8.314 x 293

number of moles n = 76350000/2436 = 31342.36 moles

We recall that n = m/MM

or m = n x MM

where

n is the number of moles

m is the mass of the gas

MM is the molar mass of the gas

For helium, the molar mass = 4 g/mol

substituting values, we have

m = 31342.36 x 4

m = 125369.44 g

m = 125.369 kg