Question

A, b, and c are collinear, and B is between a and c. The ratio of AB to AC is 1:2. If A is at (7,-1) and B is at (2,1) what are the coordinates of point C

Answer 1

C(-3,3)

Explanation:

Given

A = (7,-1)

B = (2,1)

AB:AC = 1:2

Required

Determine the coordinates of C

Since, B is between A and C; we need to determine ratio BC as follows;

`AB:AC = 1:2`

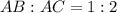
Convert to division

`(AB)/(AC) = (1)/(2)`

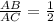
AC = AB + BC;

`(AB)/(AB + BC) = (1)/(2)`

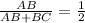
Cross Multiply

`2 * AB = 1 * (AB + BC)`

`2 AB = AB + BC`

`2AB - AB = BC`

`AB = BC`

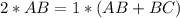
Divide both sides by BC

`(AB)/(BC) = 1`

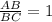
Rewrite as

`(AB)/(BC) = (1)/(1)`

Write as ratio

`AB:BC = 1:1`

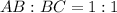
Next is to determine the coordinates of C as follows;

Because B is between both points. we have:

`B(x,y) = ((mx_2 + nx_1)/(m+n),(my_2 + ny_1)/(m+n))`

Where

`m:n = AB:BC = 1:1`

`B(x,y) = B(2,1)`

`A(x_1,y_1) = A(7,-1)`

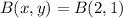
So; we're solving for x2 and y2

`B(2,1) = ((mx_2 + nx_1)/(m+n),(my_2 + ny_1)/(m+n))`

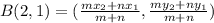
Where

Solving for x2;

`x = (mx_2 + nx_1)/(m+n)`

`2 = (1 * x_2 + 1 * 7)/(1+1)`

`2 = (x_2 + 7)/(2)`

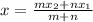
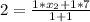
Cross Multiply

`2 * 2 = x_2 + 7`

`4 = x_2 + 7`

`x_2 = 4 - 7`

`x_2 = -3`

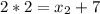
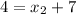
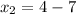
Solving for y2;

`y = (my_2 + ny_1)/(m+n)`

`1 = (1 * y_2 + 1 * -1)/(1+1)`

`1 = (y_2- 1)/(2)`

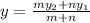
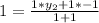
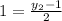
Cross Multiply

`2 * 1 = y_2 - 1`

`2 = y_2 - 1`

`y_2 = 2 + 1`

`y_2 = 3`

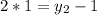
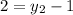
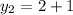
Hence, the coordinates of C are: C(-3,3)