Answer:
14
Explanation:
Perimeter of the ∆ = sum of the length of the 3 sides.
The length of the 3 sides can be calculated by using the distance formula,
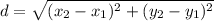 , to find the distance between the vertices of the ∆.
, to find the distance between the vertices of the ∆.
The coordinates of the 3 vertices are:
(-1, 3), (2, 2), (-2, -2)
Distance between (-1, 3) and (2, 2):
Let,
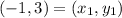
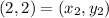
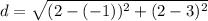
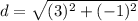
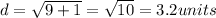
Distance between (2, 2) and (-2, -2)
Let,
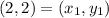
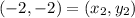
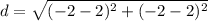
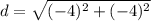
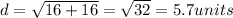
Distance between (-2, -2) and (-1, 3)
Let,
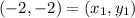
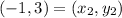
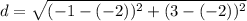
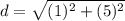

Perimeter of triangle = 3.2 + 5.7 + 5.1 = 14.0 units