Answer:
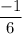
Explanation:
Given the limit of a function expressed as
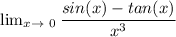 , to evaluate the following steps must be carried out.
, to evaluate the following steps must be carried out.
Step 1: substitute x = 0 into the function
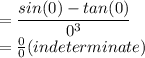
Step 2: Apply L'Hôpital's rule, by differentiating the numerator and denominator of the function
![= \lim_( x\to \ 0) ((d)/(dx)[ sin(x)-tan(x)])/((d)/(dx) (x^3))\\= \lim_( x\to \ 0) (cos(x)-sec^2(x))/(3x^2)\\](https://img.qammunity.org/2021/formulas/mathematics/college/j1oujzfrb443fuqryzp3hi5h7fu9nlkr58.png)
Step 3: substitute x = 0 into the resulting function
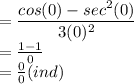
Step 4: Apply L'Hôpital's rule, by differentiating the numerator and denominator of the resulting function in step 2
![= \lim_( x\to \ 0) ((d)/(dx)[ cos(x)-sec^2(x)])/((d)/(dx) (3x^2))\\= \lim_( x\to \ 0) (-sin(x)-2sec^2(x)tan(x))/(6x)\\](https://img.qammunity.org/2021/formulas/mathematics/college/t5il8ioubi1w8q8nt5jwnfp9u6bpdeiymo.png)
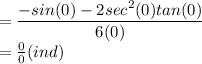
Step 6: Apply L'Hôpital's rule, by differentiating the numerator and denominator of the resulting function in step 4
![= \lim_( x\to \ 0) ((d)/(dx)[ -sin(x)-2sec^2(x)tan(x)])/((d)/(dx) (6x))\\= \lim_( x\to \ 0) ([ -cos(x)-2(sec^2(x)sec^2(x)+2sec^2(x)tan(x)tan(x)])/(6)\\\\= \lim_( x\to \ 0) ([ -cos(x)-2(sec^4(x)+2sec^2(x)tan^2(x)])/(6)\\](https://img.qammunity.org/2021/formulas/mathematics/college/39o9q47qns0n87y7ewihelqspxpbe41xm0.png)
Step 7: substitute x = 0 into the resulting function in step 6
![= ([ -cos(0)-2(sec^4(0)+2sec^2(0)tan^2(0)])/(6)\\\\= (-1-2(0))/(6) \\= (-1)/(6)](https://img.qammunity.org/2021/formulas/mathematics/college/u8i8osnv1iywzuywifdevlbungjh2qgpxo.png)
Hence the limit of the function
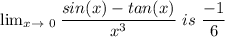 .
.