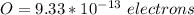Answer:
a
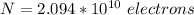
b
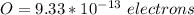
Step-by-step explanation:
From the question we are told that
The mass of the lead sphere is
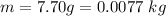
The net charge is

The atomic number is
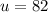
The molar mass is
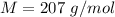
Generally the excess number of electron on the sphere is mathematically represented as
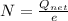
Here e is the charge on the electron is
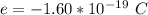
So
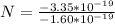
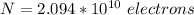
Generally the number of atom present is mathematically represented as
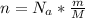
Here
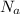 is the Avogadro's number with value
is the Avogadro's number with value
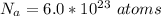
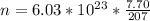
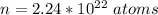
Generally the electrons are there per lead atom is mathematically represented as
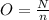
=>
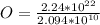
=>