Question

Find the lengths of the sides of the triangle PQR. P(4, 3, 4), Q(2, 1, 3), R(2, 7, 0) a. |PQ| = b. |QR| = c. |RP| =

Answer 1

Given :

Three points , P(4, 3, 4), Q(2, 1, 3), R(2, 7, 0) .

To Find :

The length of sides .

Given :

We know , length of two points P(x,y ,z) and Q(a,b,c) is given by :

`L=√((x-a)^2+(y-b)^2+(z-c)^2)`

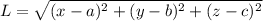
Length of PQ :

`PQ=√((4-2)^2+(3-1)^2+(4-3)^2)\\\\PQ=√(4+4+1)=√(9)\\\\PQ=3`

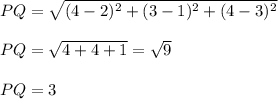
Length of QR :

`QR=√((2-2)^2+(1-7)^2+(3-0)^2)\\\\QR=√(0+6^2+3^2)\\\\QR=√(36+9)\\\\QR=√(45)\\\\QR=3√(5)` :

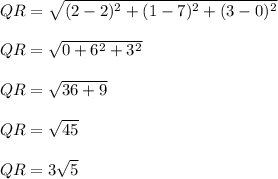Length of RP :

`RP=√((2-4)^2+(7-3)^2+(0-4)^2)\\\\RP=√(2^2+4^2+4^2)\\\\RP=√(4+16+16)\\\\RP=√(36)\\\\RP=6`

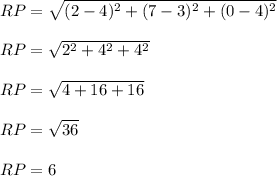
Hence , this is the required solution .