Question

Find the general solution of the following equation: y'(t) = 3y -5

Answer 1

The general solution of the equation is y =
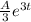`(A)/(3)e^(3t)` + 5

Explanation:

Since the differential equation is given as y'(t) = 3y -5

The differential equation is re-written as

dy/dt = 3y - 5

separating the variables, we have

dy/(3y - 5) = dt

dy/(3y - 5) = dt

integrating both sides, we have

∫dy/(3y - 5) = ∫dt

∫3dy/[3(3y - 5)] = ∫dt

(1/3)∫3dy/(3y - 5) = ∫dt

(1/3)㏑(3y - 5) = t + C

㏑(3y - 5) = 3t + 3C

taking exponents of both sides, we have

exp[㏑(3y - 5)] = exp(3t + 3C)

3y - 5 =
`e^(3t)e^(3C)`

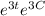
3y - 5 =
`Ae^(3t)`
`A = e^(3C)`

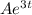
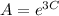
3y =
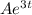`Ae^(3t)` + 5

dividing through by 3, we have

y =
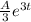`(A)/(3)e^(3t)` + 5

So, the general solution of the equation is y =
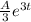`(A)/(3)e^(3t)` + 5