Determine whether each set {p1,p2} is a linearly independent set in P3. 1. The polynomials p1 (t) = 1 + t2 and p2(t) = 1 - t2. 2. The polynomials p1 (t) = 2t + t2 and p2(t) = 1 + t. 3. The polynomials - QAmmunity.org

Determine whether each set {p1,p2} is a linearly independent set in P3. 1. The polynomials p1 (t) = 1 + t2 and p2(t) = 1 - t2. 2. The polynomials p1 (t) = 2t + t2 and p2(t) = 1 + t. 3. The polynomials

asked May 10, 2021 56.3k views

1 Answer

Answer:

1) The polynomials
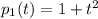p_(1)(t) = 1 +t^(2) and
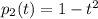p_(2)(t) = 1-t^(2) are linearly independient, 2) The polynomials
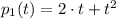$p_(1)(t) = 2\cdot t +t^(2)$ and
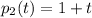p_(2)(t) = 1+t are linearly independent, 3) The polynomials
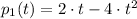$p_(1)(t) = 2\cdot t - 4\cdot t^(2)$ and
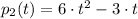$p_(2)(t) = 6\cdot t^(2)-3\cdot t$ are linearly dependent.

Explanation:

A set is linearly independent if and only if the sum of elements satisfy the following conditions:

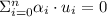
$\Sigma_(i=0)^(n) \alpha_(i) \cdot u_(i) = 0$

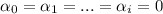
$\alpha_(0) = \alpha_(1) =...=\alpha_(i) = 0$

1) The set of elements form the following sum:

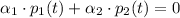
$\alpha_(1)\cdot p_(1)(t)+\alpha_(2)\cdot p_(2)(t) = 0$

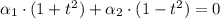
$\alpha_(1)\cdot (1+t^(2))+\alpha_(2)\cdot (1-t^(2)) = 0$

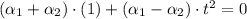
$(\alpha_(1)+\alpha_(2))\cdot (1) +(\alpha_(1)-\alpha_(2))\cdot t^(2) = 0$

From definition this system of equations must be satisfied:

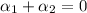$\alpha_(1) + \alpha_(2) = 0$ Eq. 1

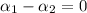$\alpha_(1)-\alpha_(2) = 0$ Eq. 2

From Eq. 2:

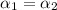
$\alpha_(1) = \alpha_(2)$

In Eq. 1:

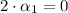
$2\cdot \alpha_(1) =0$

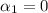
$\alpha_(1) = 0$

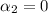
$\alpha_(2) = 0$

The polynomials
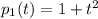p_(1)(t) = 1 +t^(2) and
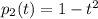p_(2)(t) = 1-t^(2) are linearly independient.

2) The set of elements form the following sum:

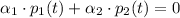
$\alpha_(1)\cdot p_(1)(t)+\alpha_(2)\cdot p_(2)(t) = 0$

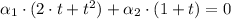
$\alpha_(1)\cdot (2\cdot t+t^(2))+\alpha_(2)\cdot (1+t) = 0$

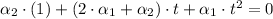
$\alpha_(2)\cdot (1) +(2\cdot \alpha_(1)+\alpha_(2))\cdot t +\alpha_1 \cdot t^(2) = 0$

From definition this system of equations must be satisfied:

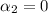
$\alpha_(2) = 0$

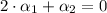
$2\cdot \alpha_(1)+\alpha_(2) = 0$

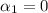
$\alpha_(1) = 0$

The polynomials
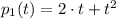$p_(1)(t) = 2\cdot t +t^(2)$ and
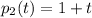p_(2)(t) = 1+t are linearly independent.

3) The set of elements form the following sum:

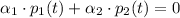
$\alpha_(1)\cdot p_(1)(t)+\alpha_(2)\cdot p_(2)(t) = 0$

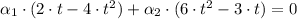
$\alpha_(1)\cdot (2\cdot t-4\cdot t^(2))+\alpha_(2)\cdot (6\cdot t^(2)-3\cdot t) = 0$

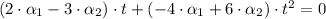
$(2\cdot \alpha_(1)-3\cdot \alpha_(2))\cdot t + (-4\cdot \alpha_(1)+6\cdot \alpha_(2))\cdot t^(2) = 0$

From definition this system of equations must be satisfied:

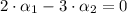$2\cdot \alpha_(1)-3\cdot \alpha_(2) = 0$ (Eq. 1)

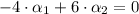$-4\cdot \alpha_(1)+6\cdot \alpha_(2) =0$ (Eq. 2)

It is easy to find that each coefficient is multiple of the other one, that is:

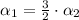$\alpha_(1) =(3)/(2)\cdot \alpha_(2)$ (From Eq. 1)

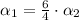$\alpha_(1) = (6)/(4)\cdot \alpha_(2)$ (From Eq. 2)

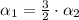
$\alpha_(1) = (3)/(2)\cdot \alpha_(2)$

Which means that polynomials
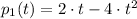$p_(1)(t) = 2\cdot t - 4\cdot t^(2)$ and
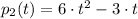$p_(2)(t) = 6\cdot t^(2)-3\cdot t$ are linearly dependent.

SvenG answered May 15, 2021

by SvenG

5.4k points

Search QAmmunity.org