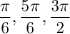Answer:
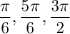
Explanation:
Given the quadratic equation as:
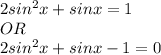
Let us put
 for simplicity of the equation:
for simplicity of the equation:
Now, the equation becomes:
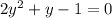
Now, let us try to solve the quadratic equation:
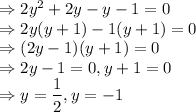
So, the solution to the given trigonometric quadratic equation is:
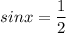
and

Let us try to find the values of
 in the interval
in the interval
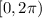 .
.
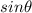 can have a value equal to
can have a value equal to
 in 1st and 2nd quadrant.
in 1st and 2nd quadrant.
So,
 can be
can be
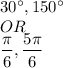
For
 ,
,

So, the answer is: