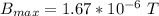Answer:
a
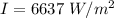
b
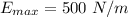
And
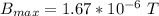
Step-by-step explanation:
From the question we are told that
The power is

The diameter is

Generally the radius is mathematically represented as
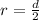
=>

=>

Generally the area of the sphere is mathematically evaluated as
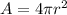
=>
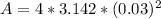
=>

Generally the total Intensity of the incandescent light bulb is mathematically represented as
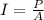
=>
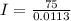
=>
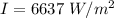
Given that 5% of the energy goes to visible light
Then the intensity that goes visible light is
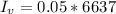
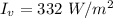
The amplitude of the electric field at the surface is mathematically represented as
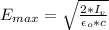
=>

=>
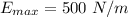
The amplitude of the magnetic field at the surface is mathematically represented as
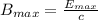
=>
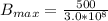
=>