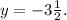Answer:
C. The focus is at
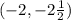 and the directrix is at
and the directrix is at
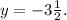
Explanation:
First of all, let us learn about the formula to find Focus and Directrix from the standard equation of a parabola.
Standard form of a parabola is given as:
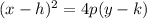
where the focus is
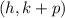 and
and
the directrix is
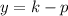
Now, we are given the equation of parabola as:
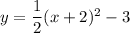
Let us try to convert it to standard form:
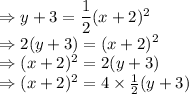
Comparing the above with standard equation of parabola
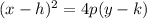 :
:

So, Focus is at
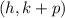
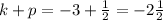
Focus is at
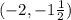 .
.
Equation of directrix:
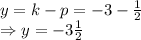
Also, please refer to the attached image for the diagram of given parabola, focus and directrix.
So, the answer is:
C. The focus is at
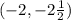 and the directrix is at
and the directrix is at