Answer:
474 grams of chlorine gas are present in a 150 liter cylinder of chlorine held at a pressure of 1.00 atm and 0 °C
Step-by-step explanation:
An ideal gas is a theoretical gas that is considered to be composed of randomly moving point particles that do not interact with each other. Gases in general are ideal when they are at high temperatures and low pressures.
The pressure, P, the temperature, T, and the volume, V, of an ideal gas, are related by a simple formula called the ideal gas law:
P*V = n*R*T
where P is the gas pressure, V is the volume that occupies, T is its temperature, R is the ideal gas constant, and n is the number of moles of the gas.
In this case:
- P= 1.00 atm
- V= 150 L
- n= ?
- R= 0.082
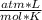
- T= 0 C= 273 K
Replacing:
1.00 atm* 150 L= n*0.08206
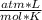 *273 K
*273 K
Solving:
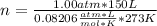
n= 6.69 moles
Being Cl= 35.45 g/mole, the molar mass of chlorine gas is:
Cl₂=2*35.45 g/mole= 70.9 g/mole
So if 1 mole has 70.9 grams, 6.69 moles of the gas, how much mass does it have?
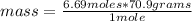
mass= 474.321 grams ≅ 474 grams
474 grams of chlorine gas are present in a 150 liter cylinder of chlorine held at a pressure of 1.00 atm and 0 °C