Complete Question
The complete question is shown on the first uploaded image
Answer:
A
is dimensionally consistent
B
is not dimensionally consistent
C
is dimensionally consistent
D
is not dimensionally consistent
E
is not dimensionally consistent
F
is dimensionally consistent
G
is dimensionally consistent
H
is not dimensionally consistent
Step-by-step explanation:
From the question we are told that
The equation are
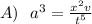
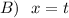
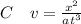
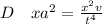
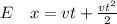
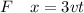
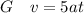
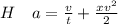
Generally in dimension
x - length is represented as L
t - time is represented as T
m = mass is represented as M
Considering A
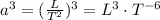
and
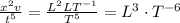
Hence
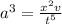 is dimensionally consistent
is dimensionally consistent
Considering B
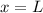
and
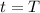
Hence
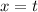 is not dimensionally consistent
is not dimensionally consistent
Considering C
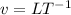
and
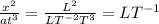
Hence
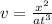 is dimensionally consistent
is dimensionally consistent
Considering D

and
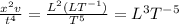
Hence
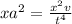 is not dimensionally consistent
is not dimensionally consistent
Considering E
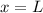
;
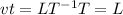
and
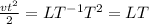
Hence
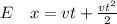 is not dimensionally consistent
is not dimensionally consistent
Considering F
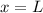
and
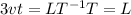 Note in dimensional analysis numbers are
Note in dimensional analysis numbers are
not considered
Hence
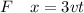 is dimensionally consistent
is dimensionally consistent
Considering G
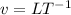
and
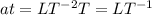
Hence
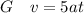 is dimensionally consistent
is dimensionally consistent
Considering H
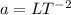
,
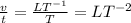
and
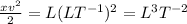
Hence
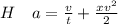 is not dimensionally consistent
is not dimensionally consistent