Answer:
a
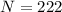
b
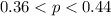
c
No we can not safely conclude that majority of students enjoy statistics because the upper limit of the confidence level is less than 50%
Explanation:
From the question we are told that
The sample size is
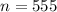
The percentage that enjoyed statistics is
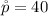
Generally the number of student who say they enjoyed statistics is mathematically represented as
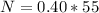
=>
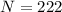
Given that the confidence level is 95% then the level of significance is mathematically represented as
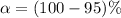
=>

The critical value of
 obtained from the normal distribution table is
obtained from the normal distribution table is
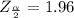
The margin of error is mathematically represented as

=>

=>.
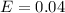
The 95% confidence interval is mathematically represented as
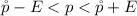
=>
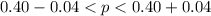
=>
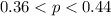
No we can not safely conclude that majority of students enjoy statistics because the upper limit of the confidence level is less than 50%