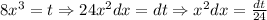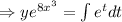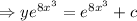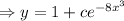Question

Match the following differential equations with their solutions. The symbols A, B, C in the solutions stand for arbitrary constants. You must get all of the answers correct to receive credit.

1. d^2y/dx^2 + 25y = 0
2. dy/dx = 2xy/x^2 - 5y^2
3. d62y/dx^2 + 16 dy/dx + 64y = 0
4. dy/dx = 10xy
5. dy/dx + 24x^2y = 24 x^2
A. y = Ce^-8x^3 + 1
B. 3yx^2 - 5y^3 = C
C. y = Ae^-8x + Bxe^-8x
D. y = Ae^5x^2
E. y = A cos(5x) + B sin(5x)

Answer 1

`1 \rightarrow E, 2\rightarrow B, 3\rightarrow C, 4\rightarrow D, 5\rightarrow A`

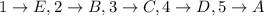
Explanation:

1.
`(d^2y)/(dx^2)+25y=0`

The characteristic equation for the given differential equation is:

`r^(2) +25=0`

`\Rightarrow r^2=-25`

`\Rightarrow r=\pm 5i`

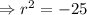
Since the roots are complex

Now, the general solution is:

`y=A\cos 5x+B\sin 5x`

2.
`(dy)/(dx)=\frac {2xy}{x^2}-5y^2`

`\Rightarrow (dy)/(dx)-\frac 2xy=-5y^2`

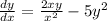
Divide both sides by
`y^(-1)`

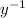
Let,
`v=y^(-1) \Rightarrow (dv)/(dx)=-y^(-2)(dy)/(dx)`

`\Rightarrow -(dv)/(dx)-\frac 2xv=-5`

`\Rightarrow (dv)/(dx)+\frac 2xv=5`

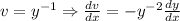
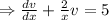
Here,
`p(x)=\frac 2x\; \text{and}\;\; q(x)=5`

I.F.
`=e^(\int \frac 2xdx)=x^2`

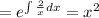
Now, the general solution is:

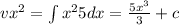
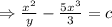
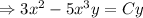
`vx^2=\int x^2 5dx=\frac {5x^3}3+c`

`\Rightarrow \frac {x^2}y-\frac {5x^3}3=c`

`\Rightarrow 3x^2-5x^3y=Cy`

3.
`(d^2y)/(dx^2)+16(dy)/(dx)+64y=0`

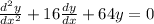
The characteristic equation is:

`r^2+16r+64=0`

`\Rightarrow r^2+8r+8r+64=0`

`\Rightarrow r(r+8)+8(r+8)=0`

`\Rightarrow (r+8)(r+8)=0`

`\Rightarrow r=-8,-8`

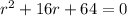
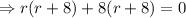
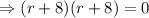
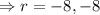
Since the roots are real and repeated.

Now, the general solution is:

`y=Ae^(-8x)+Bxe^(-8x)`

4.
`\frac {dy}{dx}=10xy`

`\Rightarrow \frac {dy}{y}=10xdx`

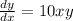
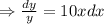
Integrating both sides

`\int\frac {dy}y=\int 10xdx+\log c`

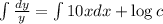
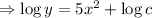
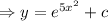
`\Rightarrow \log y=5x^2+\log c`

`\Rightarrow y=e^(5x^2)+c`

5.
`\frac {dy}{dx}+24x^2y=24x^2`

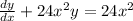
Here,
`p(x)=24x^2 \; \text{and}\;\; q(x)=24x^2`

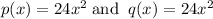
I.F.
`= e^(\int 24x^2dx)=e^(8x^3)`

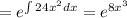
Now, the general solution is:

`y.e^(8x^3)=\int 24x^2 e^(8x^3)dx=24\int x^2e^(8x^3)dx`

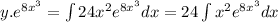
Let,
`8x^3=t \Rightarrow 24x^2dx=dt\Rightarrow x^2dx=\frac {dt}{24}`

`\Rightarrow ye^(8x^3)=\int e^tdt`

`\Rightarrow ye^(8x^3)=e^(8x^3)+c`

`\Rightarrow y=1+ce^(-8x^3)`