Question

If A=kr² and V=kr³, find the percentage increase in A and V if r is increased by 20%​

Answer 1

The percentage increase in A is 44%. The percentage increase in V is 72.8%.

Explanation:

The easiest way to go about solving this problem is to pick your own numbers and plug them into the given equations.

For example, let's say that k = 5 and that r = 10.

`A=kr^(2)` ⇒
`A= 5 * 10^(2) =500`

`V=kr^(3)` ⇒
`V= 5 * 10^(3)= 5000`

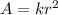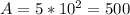
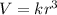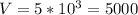
The question is asking, what is the percentage increase if r is increased by 20%. Our chosen k-value will stay the same but our r-value is going to increase. To find the new value of r, we multiply 10, our current value of r, by 1.2. This gives us a new value for r, which is 12.

`10*1.2=12`

Now, we are going to plug in our new r-value and our k-value into the given equations. k = 5; new r = 12

`A=kr^(2)` ⇒
`A=5*12^(2)=720`

`V=kr^(3)` ⇒
`V=5*12^(3)=8640`

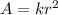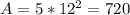
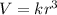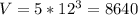
Next, we have to calculate the percentage increase in our values of A and V. To do this, we use the following formula:

`Percentage Increase = (final - initial)/(initial) * 100`

Percentage Increase for A

Initial value: 500

Final Value: 720

`Percentage Increase = (720-500)/(500) * 100 = 44%`

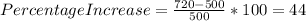
Percentage Increase for V

Initial value: 5000

Final Value: 8640

`Percentage Increase= (8640-5000)/(5000) *100 = 72.8%`

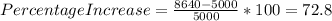
The percentage increase for A is 44% and the percentage increase for V is 72.8%.

Hope this helps!