Question

On a coordinate plane, kite W X Y Z is shown. Point W is at (negative 3, 3), point X is at (2, 3), point Y is at (4, negative 4), and point Z is at (negative 3, negative 2). What is the perimeter of kite WXYZ? units units units units

Answer 1

C is the answer.

That is all.

Answer 2

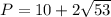`P = 10 + 2√(53)` units

Explanation:

Given

Shape: Kite WXYZ

W (-3, 3), X (2, 3),

Y (4, -4), Z (-3, -2)

Required

Determine perimeter of the kite

First, we need to determine lengths of sides WX, XY, YZ and ZW using distance formula;

`d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)`

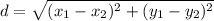
For WX:

`(x_1, y_1)\ (x_2,y_2) = (-3, 3),\ (2, 3)`

`WX = √((-3 - 2)^2 + (3 - 3)^2)`

`WX = √((-5)^2 + (0)^2)`

`WX = √(25)`

`WX = 5`

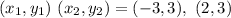
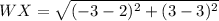
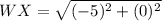
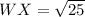
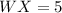
For XY:

`(x_1, y_1)\ (x_2,y_2) = (2, 3)\ (4,-4)`

`XY = √((2 - 4)^2 + (3 - (-4))^2)`

`XY = √(-2^2 + (3 +4)^2)`

`XY = √(-2^2 + 7^2)`

`XY = √(4 + 49)`

`XY = √(53)`

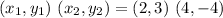
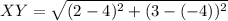
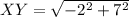
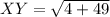
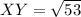
For YZ:

`(x_1, y_1)\ (x_2,y_2) = (4,-4)\ (-3, -2)`

`YZ = √((4 - (-3))^2 + (-4 - (-2))^2)`

`YZ = √((4 +3)^2 + (-4 +2)^2)`

`YZ = √(7^2 + (-2)^2)`

`YZ = √(49 + 4)`

`YZ = √(53)`

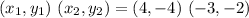
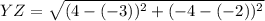
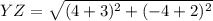
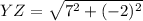
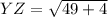
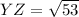
For ZW:

`(x_1, y_1)\ (x_2,y_2) = (-3, -2)\ (-3, 3)`

`ZW = √((-3 - (-3))^2 + (-2 - 3)^2)`

`ZW = √((-3 +3)^2 + (-2 - 3)^2)`

`ZW = √(0^2 + (-5)^2)`

`ZW = √(0 + 25)`

`ZW = √(25)`

`ZW = 5`

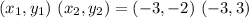
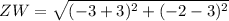
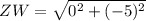
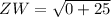
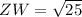
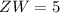
The Perimeter (P) is as follows:

`P = WX + XY + YZ + ZW`

`P = 5 + √(53) + √(53) + 5`

`P = 5 + 5 + √(53) + √(53)`

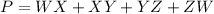
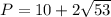`P = 10 + 2√(53)` units