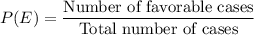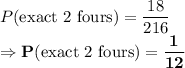Question

Toss 3 dice. What's the probability that a 4 will come up exactly twice?

Answer 1

To find the probability of getting a 4 exactly twice when tossing 3 dice, we need to calculate the number of favorable outcomes and divide it by the total number of possible outcomes. The probability is approximately 0.0694 or 6.94%.

Step-by-step explanation:

To find the probability of getting a 4 exactly twice when tossing 3 dice, we need to calculate the number of favorable outcomes and divide it by the total number of possible outcomes.

There are 3 ways to choose which 2 out of the 3 dice will show a 4. For each of these 2 dice that show a 4, there are 5 other numbers that can appear on the remaining die. Therefore, the number of favorable outcomes is 3 * 5 = 15.

The total number of possible outcomes when tossing 3 dice is 6^3 = 216.

Therefore, the probability of getting a 4 exactly twice when tossing 3 dice is 15/216, which simplifies to approximately 0.0694 or 6.94%.

Answer 2

`\bold{(1)/(12)}`

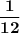
Step-by-step explanation:

The dice is rolled 3 times.

To find:

The probability that a 4 will come up exactly twice = ?

Solution:

Let 4 comes up exactly twice, let the third number be
`x`.

The possible outcomes can be:

(
`x`, 4, 4) where
`x` can be any number between 1 to 6 , so 6 outcomes.

(4,
`x`, 4) where
`x` can be any number between 1 to 6 , so 6 outcomes.

(4, 4,
`x`) where
`x` can be any number between 1 to 6 , so 6 outcomes.

So, the total number of favorable outcomes possible = 6 + 6 + 6 = 18

Total number of outcomes that can be possible at roll of 3 dice:

6
`*` 6
`*` 6 = 216

Formula for probability of an event E is given as:

`P(E) = \frac{\text{Number of favorable cases}}{\text {Total number of cases}}`

`P(\text{exact 2 fours}) = (18)/(216)\\\Rightarrow \bold{P(\text{exact 2 fours}) = (1)/(12)}`