Question

In each problem 7 through 14, verify that each given function is a solution of the differential equation. Y" - y = 0; y1(t) = et, y2(t) = cosh t.

Answer 1

Since L.H.S = R.H.S = 0, for both
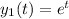`y_(1) (t) = e^(t)` and
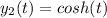`y_(2) (t) = cosh(t)`, y₁ and y₂ both satisfy the equation y" - y = 0 and are thus solutions to the differential equation.

Explanation:

To check whether the given functions are solutions the given differential equation, we differentiate the functions and then insert it into the given equation.

So y" - y = 0 and

`y_(1) (t) = e^(t)\\y_(1)' (t) = e^(t)\\ y_(1)`

Substituting these values of y and y" into the left hand side of the equation, we have

y" - y

`y_(1)`

Since L.H.S = R.H.S

So
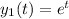`y_(1) (t) = e^(t)` is a solution of the differential equation.

When

`y_(2) (t) = cosh(t)\\ y_(2)'(t) = sinh(t) \\y_(2)`

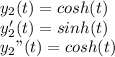
Substituting y and y" into the left hand side of the equation, we have

y" - y

`y_(2)`

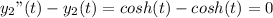
Since L.H.S = R.H.S

So,
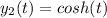`y_(2) (t) = cosh(t)` is a solution of the differential equation.