Answer:
Function:
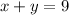
Not Function:
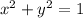 and
and
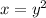
Explanation:
Given
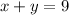
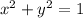
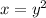
Required
Determine if
 is a function of
is a function of

Solving x+y=9
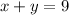
Make y the subject of formula
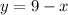
Hence; y is a function of x
Solving
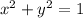
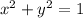
Subtract x² from both sides
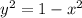
Square root of both sides
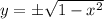
This implies that
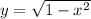 or
or

Because
 can be any of those two expressions, it is not a function.
can be any of those two expressions, it is not a function.
Solving
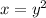
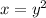
Reorder

Take square roots

This implies that
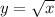 or
or
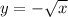
Because
 can be any of those two expressions, it is not a function.
can be any of those two expressions, it is not a function.