Question

a sequence of numbers begins at 400. If the pattern increases by consecutive multiples of 5 starting with 5, then find the next 3 numbers in the sequence 400, ___, ___, ___, ...

Answer 1

Given :

A sequence of numbers begins at 400.

To Find :

If the pattern increases by consecutive multiples of 5 starting with 5, then find the next 3 numbers in the sequence 400, ___, ___, ___ .

Solution :

This is the a question of arithmetic progression .

The first term is , a = 400 .

Now , it is given that the next numbers increase by the multiples of 5 starting with 5 .

So , common difference is , d = 5 .

Now , we know ,
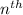`n^(th)` number in A.P is given by :

`a_n=a+(n-1)d`

Putting value of n = 2 , 3 , 4 .

We get :

`a_2=a+(2-1)d=400+5=405\\\\a_3=a+(3-1)d = 400 + (5* 2) = 410\\\\a_4=a+(4-1)d = 400 +(5* 3)=415`

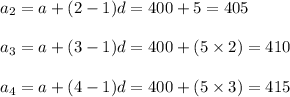
Therefore , the next 3 numbers in the sequence is 400 , 405 , 410 , 415 .

Hence , this is the required solution .