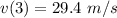Question

Use the position function s(t) = –4.9t2 + 500, which gives the height (in meters) of an object that has fallen for t seconds from a height of 500 meters. The velocity at time t = a seconds is given by the following.

lim t->a: (s(a) - s(t)) / (a - t)
Find the velocity of the object when t = 3. (Round your answer to two decimal places.)

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

The value is
`v(3) =  29.4 \  m/s`

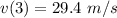
Explanation:

From the question we are told that

`s(t) =  -4.9t^2 + 500`

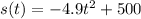
And

`\lim_(t \to a)  (s(a) - s(t))/(a-t)`

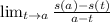
Generally s(t) at t = a is mathematically evaluated as

`s(a) =  -4.9a^2+ 500`

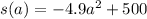
So

`s(a) - s(t) =  -4.9a^2 + 500 - ( -4.9t^2+500)`

`s(a) - s(t) =  -4.9a^2 + 500 +4.9t^2-500)`

`s(a) - s(t) = 4.9(t^2 - a^2)`

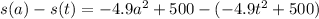
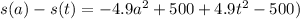
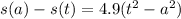
Thus the velocity is represented as

`v(t) =\lim_(t \to a)  (s(a) - s(t))/(a-t) \equiv \lim_(t \to a) (4.9(t^2 -  a^2 ))/( a-t)`

=>
`v(t) = \lim_(t \to a)  - 4.9(a + t )`

=>
`v(t) = -4.9 (a + a )`

=>
`v(t) = -9.8a`

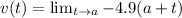
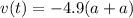
Now at t = 3

=>
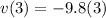
`v(3) = -9.8 (3)`

=>
`v(3) =  29.4 \  m/s`