Question

Can y’all help me plss

Answer 1

It should be noted that the opposite angles of a parallelogram are equivalent. Therefore, ∠A = ∠C and ∠B = ∠D.

Given:

• ∠A = 7z + 5
• ∠B = 5w - 30
• ∠C = 8z - 10
• ∠D = 3w + 10

Therefore, we obtain the following equations;

⇒ 7z + 5 = 8z - 10 and 5w - 30 = 3w + 10

Let us simplify each equation one by one.

7z + 5 = 8z - 10:

• ⇒ 7z + 5 = 8z - 10
• ⇒ 7z + 5 - 5 = 8z - 10 - 5 (Subtract 5 both sides)
• ⇒ 7z = 8z - 15 (Simplify both sides)
• ⇒ 7z - 8z = 8z - 15 - 8z (Subtract 8x both sides)
• ⇒ z = 15 (Simplify both sides)

5w - 30 = 3w + 10:

• ⇒ 5w - 30 = 3w + 10
• ⇒ 5w - 30 - 3w = 3w + 10 - 3w (Subtract 3w both sides)
• ⇒ 2w - 30 = 10 (Simplify both sides)
• ⇒ 2w - 30 + 30 = 10 + 30 (Add 30 both sides)
• ⇒ 2w = 40 (Simplify both sides)
• ⇒ 2w/2 = 40/2 (Divide 2 both sides)
• ⇒ w = 20 (Simplify both sides)

Answer 2

In a parallelogram,

⇒the angles adjacent to each other

⇒ are of the same measure

⇒so

∠A = ∠C

∠B = ∠D

Let's solve:

• ∠A = ∠C

`7z +5 = 8z - 10\\5+10=8z-7z\\8z-7z=5+10\\z = 15`

• ∠B = ∠D

`5w-30=3w+10\\5w-3w=30+10\\2w = 40\\w=20`

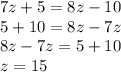
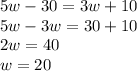
Let's check:

⇒ for all quadrilaterals like a parallelogram

⇒all the angle measures added up to 360, so:

`(7z+5)+(8z-10)+(5w-30)+(3w+10)=360\\(7(15)+5)+(8(15)-10)+(5(20)-30)+(3(20)+10)=360\\(105+5)+(120-10)+(100-30)+(60+10)=360\\110+110+70+70=360\\220+140=360\\360=360`

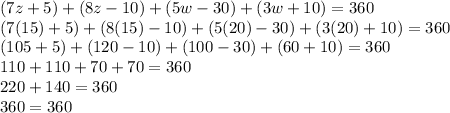
Thus:

Answer: w = 20 and z = 15

Hope that helps!