Question

What would the force of the Earth on the moon be when the moon is 2.0D from the Earth?

Answer 1

Force,
`F=7.3* 10^(36)\ N`

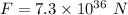
Step-by-step explanation:

We need to find the force of the Earth on the moon be when the moon is 2.0D from the Earth.

The force that act between Earth and the Moon is gravitational force. It is given by :

`F=(Gm_1m_2)/(r^2)`

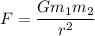
We have,

`m_1=\text{mass of Earth}=5.972 * 10^(24)\ kg`

`m_2=\text{mass of Moon}=7.34* 10^(22)\ kg`

So,

`F=(6.67* 10^(-11)* 5.972 * 10^(24)* 7.34* 10^(22))/((2)^2)\\\\F=7.3* 10^(36)\ N`

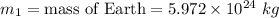
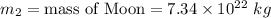
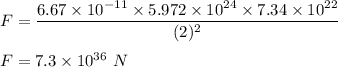
So, the force of the Earth on the Moon is
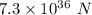`7.3* 10^(36)\ N`.