Question

Use area of squares to visualize Pythagorean theorem

The diagram shows a right triangle and three squares. The area of the largest square is 55 units.

Answer 1

A. 12 and 43

Explanation:

Pythagorean theorem is given as =
`a^2 + b^2 = c^2`

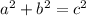
Where, a and b are the two legs of the right triangle, while c is the hypotenuse/longest leg of the triangle.

In the figure given, the side of the largest square = the hypotenuse of the triangle = c

While the side of the other squares = a and b respectively, of the triangle.

Area of square = s², where s is the side length of the square.

Since we are given that the area of the largest square = 55, this is also equivalent to c² in the Pythagorean theorem.

The side length of the largest square = √55 ≈ 7.4 = c

Therefore, to determine the area of the other squares, check the options given if they add up to give 55.

Option A: 12 + 43 = 55

Option B: 14 + 40 = 54

Option C : 16 + 37 = 53.

The correct possible areas of the smaller squares would be A. 12 and 43.