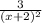Question

Q:Resolve this into partial fraction.
9/(X-1)(X+2)^2

Answer 1

`(1)/(x-1)` -
`(1)/(x+2)` -
`(3)/((x+2)^2)`

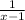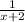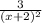
Explanation:

Expressing as a partial fraction

`(9)/((x-1)(x+2)^2)` =
`(A)/((x-1))` +
`(B)/((x+2))` +
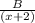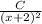`(C)/((x+2)^2)` ( A, B, C are numerical values to be found )

Multiply both sides by (x - 1)(x + 2)²

9 = A(x + 2)² + B(x - 1)(x + 2) + C(x - 1)

Choose value for x that are zeros of the factors and substitute into right side

x = - 2 : 9 = - 3C ⇒ C = - 3

x = 1 : 9 = 9A ⇒ A = 1

x = 0 : 9 = 4A - 2B - C , that is

9 = 4 - 2B + 3 = - 2B + 7 ( subtract 7 from both sides )

2 = - 2B ⇒ B = - 1, then

A = 1, B = - 1, C = - 3

Thus

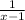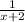`(9)/((x-1)(x+2)^2)` =
`(1)/(x-1)` -
`(1)/(x+2)` -
`(3)/((x+2)^2)`