Question

A particle moves along the x-axis according to the equation

S = 4+6t-2t^2
where S is in meters and t is in seconds. At t = 3.0 s, calculate
(a) the position of the particle
(b) its instantaneous velocity
(c) its instantaneous acceleration.​

Answer 1

◈ A particle is moving along the x-axis according to the equation

• S = 4 + 6t - 2t²

____________________________

✪ Position at t = 3s :

➝ S = 4 + 6t - 2t²

➝ S = 4 + 6(3) - 2(3)²

➝ S = 4 + 18 - 18

➝ S = 4m

✪ Instantaneous velocity at t = 3s :

➝ v = dx/dt = d(4 + 6t - 2t²)/dt

➝ v = 6 - 4t

➝ v = 6 - 4(3)

➝ v = 6 -
`\sf{12}`

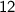
➝ v = -12m/s

✪ Instantaneous acc. at t = 3s :

➝ a = dv/dt = d(6 - 4t)/dt

➝ a = -4m/s²

[Acceleration does not depend on time]