Question

What is the car's average velocity (in m/s) in the interval between t = 0.5 s
to t = 2 s?

Answer 1

`1.0\; \rm m \cdot s^(-1)`.

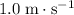Step-by-step explanation:

Consider a time period of duration
`\Delta t`. Let change in the position of an object during that period of time be denoted as
`\Delta x`. The average velocity of that object during that period would be:

`\displaystyle \bar{v} = (\Delta x)/(\Delta t)`.

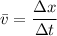For the toy car in this question, the time interval has a duration of
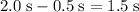`2.0 \; \rm s - 0.5\; \rm s = 1.5\; \rm s`. That is:
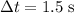`\Delta t = 1.5\; \rm s`. (One decimal place, two significant figures.)

On the other hand, what would be the change in the position of this toy car during that
`1.5\; \rm s`?

Note, that from readings on the snapshot in the diagram:

• The position of the toy car was
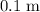  `0.1\; \rm m` at
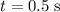  `t = 0.5\; \rm s` (the beginning of this
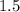  `1.5`-second time period.)
• The position of the toy car was
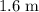  `1.6\; \rm m` at
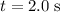  `t = 2.0\; \rm s` (the end of this
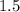  `1.5`-second time period.)

Therefore, the change to the position of this toy car over that time period would be
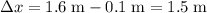`\Delta x = 1.6\; \rm m - 0.1\; \rm m = 1.5\; \rm m`. (One decimal place, two significant figures.)

The average velocity of this car over this period of time would thus be:

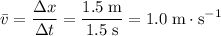`\displaystyle \bar{v} = (\Delta x)/(\Delta t) = (1.5\; \rm m)/(1.5\; \rm s) = 1.0\; \rm m \cdot s^(-1)`. (Two significant figures.)