Question

Find a formula for the inverse of the function. f(x) = e^6x − 9

Answer 1

`f^(-1)(x)=(1)/(6)\ln(x+9)`

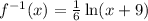
Explanation:

So we have the function:

`f(x)=e^(6x)-9`

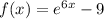
To solve for the inverse of a function, change f(x) and x, change the f(x) to f⁻¹(x), and solve for it. Therefore:

`x=e^{6f^(-1)(x)}-9`

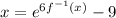
Add 9 to both sides:

`x+9=e^{6f^(-1)(x)}`

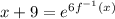
Take the natural log of both sides:

`\ln(x+9)=\ln(e^{6f^(-1)(x)})`

The right side cancels:

`\ln(x+9)=6f^(-1)(x)`

Divide both sides by 6:

`f^(-1)(x)=(1)/(6)\ln(x+9)`

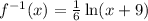
And we're done!