Question

Write an equation in slope intercept format of the line that is a segment bisector of both AB and CD. A(-1,8) B(3,4) C(1,10) and D(7,8) find y. ​

Answer 1

y = x + 5

Step-by-step explanation:

The equation of a line in slope intercept form is y = mx + c, where m is the slope and y is the intercept

The midpoint or bisector (x, y) of a line with endpoints at (
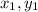`x_1,y_1`) and (
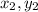`x_2,y_2`) is given by:

`x=(x_1+x_2)/(2)\\ \\y=(y_1+y_2)/(2)`

If AB is at A(-1,8) B(3,4), the coordinates of the midpoint of AB is:

`x=(x_1+x_2)/(2)=(-1+3)/(2)=1 \\ \\y=(y_1+y_2)/(2)=(8+4)/(2) =6`

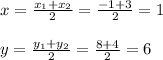
The midpoint of AB is (1, 6)

If CD is at C(1,10) and D(7,8), the coordinates of the midpoint of CD is:

`x=(x_1+x_2)/(2)=(1+7)/(2)=4 \\ \\y=(y_1+y_2)/(2)=(10+8)/(2) = 9`

The midpoint of CD is (4, 9)

The equation of the line passing through two points is given as:

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)\\ \\The \ equation \ of\ the\ line \ passing\ through \ the\ midpoint\ of\ AB, i.e (1,6)\ \\and\ the\ mdpoint\ of\ CD\ i.e(4,9)\ is:\\\\y-6=(9-6)/(4-1)(x-1)\\ \\y-6=1(x-1)\\\\y=x-1+6\\\\y=x+5`