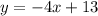Answer:
Explanation:
We are given the two points (3, 1) and (2, 5) and we want to find the equation of the line containing the given points.
First, find the slope of the line:
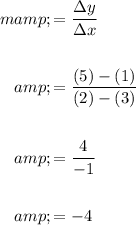
Hence, the slope of the line is -4.
Since we know the slope and a point, we can consider using the point-slope form, given by:

Let's use (3, 1) as the chosen point, and we will substitute -4 for the slope m. This yields:
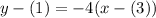
To convert into slope-intercept form, solve for y:
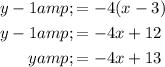
In conclusion, the equation of the line is: