Question

8) Find the endpoint Cif M is the midpoint of segment CD and M (2, 4) and D (5,7)

a) (-3,-3) b) (-2,-1) c) (-1,1) d) (2,4)

Answer 1

8. c. (-1, -1)

9. a. (-6, -1)

b. True

Explanation:

8. Given the midpoint M(2, 4), and one endpoint D(5, 7) of segment CD, the coordinate pair of the other endpoint C, can be calculated as follows:

let
`D(5, 7) = (x_2, y_2)`

`C(?, ?) = (x_1, y_1)`

`M(2, 4) = ((x_1 + 5)/(2), (y_1 + 7)/(2))`

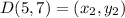
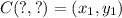
Rewrite the equation to find the coordinates of C

`2 = (x_1 + 5)/(2)` and
`4 = (y_1 + 7)/(2)`

Solve for each:

`2 = (x_1 + 5)/(2)`

`2*2 = (x_1 + 5)/(2)*2`

`4 = x_1 + 5`

`4 - 5 = x_1 + 5 - 5`

`-1 = x_1`

`x_1 = -1`

`4 = (y_1 + 7)/(2)`

`4*2 = (y_1 + 7)/(2)*2`

`8 = y_1 + 7`

`8 - 7 = y_1 + 7 - 7`

`1 = y_1`

`y_1 = 1`

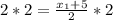
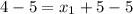
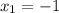
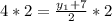
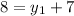
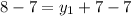
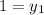
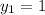
Coordinates of endpoint C is (-1, 1)

9. a.Given segment AB, with midpoint M(-4, -5), and endpoint A(-2, -9), find endpoint B as follows:

let
`A(-2, -9) = (x_2, y_2)`

`B(?, ?) = (x_1, y_1)`

`M(-4, -5) = ((x_1 + (-2))/(2), (y_1 + (-9))/(2))`

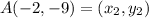
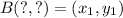
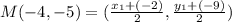
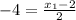`-4 = (x_1 - 2)/(2)` and
`-5 = (y_1 - 9)/(2)`

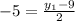
Solve for each:

`-4 = (x_1 - 2)/(2)`

`-4*2 = (x_1 - 2)/(2)*2`

`-8 = x_1 - 2`

`-8 + 2 = x_1 - 2 + 2`

`-6 = x_1`

`x_1 = -6`

`-5 = (y_1 - 9)/(2)`

`-5*2 = (y_1 - 9)/(2)*2`

`-10 = y_1 - 9`

`-10 + 9 = y_1 - 9 + 9`

`-1 = y_1`

`y_1 = -1`

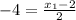
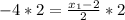
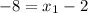
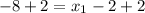
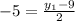
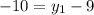
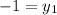
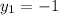
Coordinates of endpoint B is (-6, -1)

b. The midpoint of a segment, is the middle of the segment. It divides the segment into two equal parts. The answer is TRUE.