===================================

- Two ladders are leaning against a wall as shown, making the same angle with the ground. The longer ladder reaches 40 feet up the wall. How far up the wall does the short ladder reach?
===================================

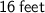
===================================

Setting up the equation, establish the best proportion.
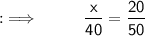
Solving the equation, setting up the ratios and then cross multiply.
Hence, the short ladder reach the wall up to 16 feet.
===================================