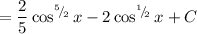Question

Calculus 2 master needed; evaluate the integral PLEASE SHOW STEPS IF IM WRONG
`\int{sin^3x/√(cosx) } \, dx` I split off the sin^3 so i can use the pythag identity and allows for u substitution u=cosx du=-sinx dx -du=sin dx
`\int{1-u^2/√(u)*-du }` I move the negative towards the outside of the integral. then i divide the terms by sqroot 2|||
`-\int{(1/√(u) - u^2/√(u) )} \, du` I eventually get to a=1/2 b =5/2
`-2{cos^a x +2/5cos^b} \, dx` did I miss anything? Or is this the final answer?

Answer 1

= - 2
`√(cos(x))` + 2 cos⁵/₂ (x) + C

5

Explanation:

∫ sin³ (x) dx

`√(cos(x))`

= ∫ sin² (x) sin (x) dx

`√(cos(x))`

= ∫ (1 - cos² (x) sin (x) dx

`√(cos(x))`

= ∫ - 1 - u² du

√u

= ∫ - 1 + u³/₂ du

√u

= - ∫ 1 du + ∫ u³/₂ du

√u

substitute it back

= - 2 √u + 2 cos⁵/₂ (x)

5

add constant, therefore

= - 2
`√(cos(x))` + 2 cos⁵/₂ (x) + C

5

Answer 2

Your process is indeed correct!

The full solution is:

`\displaystyle \int(\sin ^3 x)/(√(\cos x))\, dx= (2)/(5) \cos^{{}^(5)\!/\!{}_(2)} x - 2\cos ^{{}^(1)\!/\!{}_(2)}x + C`

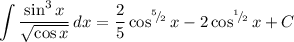
Explanation:

We want to evaluate the integral:

`\displaystyle \int (\sin^3(x))/(√(\cos(x)))\, dx`

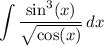
As you had done, we can rewrite our integral as:

`\displaystyle =\int (\sin(x)(\sin^2(x)))/(√(\cos(x)))\, dx`

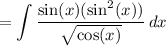
Using the Pythagorean Identity, this is:

`\displaystyle =\int (\sin(x)(1-\cos^2(x)))/(√(\cos(x)))\, dx`

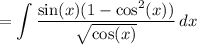
Now, we can make a substitution. Let u = cos(x). Then:

`\displaystyle du = - \sin x \, dx`

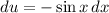
Substitute:

`\displaystyle = \int(1-u^2)/(√(u)) \, \left(- du\right)`

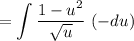
Simplify:

`\displaystyle = -\int (1)/(√(u)) - (u^2)/(√(u))\, du`

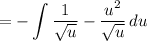
Rewrite:

`\displaystyle = -\int u^{{}^(-1)\!/\!{}_(2)} - u^{{}^(3)\!/\!{}_(2)}\, du`

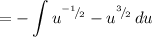
By the Reverse Power Rule:

`\displaystyle = -\left(2u^{{}^(1)\!/\!{}_(2)} - (2)/(5) u^{{}^(5)\!/\!{}_(2)}\right) + C`

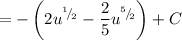
Simplify:

`\displaystyle = (2)/(5) u^{{}^(5)\!/\!{}_(2)}-2u^{{}^(1)\!/\!{}_(2)} + C`

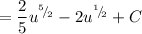
Back-substitute:

`\displaystyle = (2)/(5) \cos^{{}^(5)\!/\!{}_(2)} x - 2\cos ^{{}^(1)\!/\!{}_(2)}x + C`