Answer:
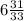
This is a mixed number where the whole part is 6, and the fractional part is 31/33.
=============================================
Step-by-step explanation:
The 93 repeats forever, so we can say
x = 6.939393...
100x = 693.939393....
Subtracting the left hand sides leads to 100x-x = 99x
Subtracting the right hand sides leads to 693.939393.... - 6.939393... = 687
Notice how the decimal terms cancel out when we subtract.
We're left with 99x = 687 which solves to x = 687/99
This reduces to 229/33 when you divide both parts by 3.
The last step is to convert to a mixed number
The answer will be in the form
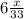 where 6 is the whole part and x/33 is the fractional part. We know the whole part is 6 from the 6 in the original number given.
where 6 is the whole part and x/33 is the fractional part. We know the whole part is 6 from the 6 in the original number given.
229/33 = 6.939393... helps confirm we're on the right track so far
this is another way of saying 229/33 = 6 remainder x, where x is the unknown remainder and the numerator we're after for the fraction x/33.
To get the remainder, we just compute 229-6*33 to get 31
This means 31/33 = 0.93939393...
and that
