Question

A rectangle has an area of 60 cm2. Its width is 7 cm less than its length. (a) Let x cm be the length of the rectangle. Write an equation using the rectangle's area. (b) Solve your equation for x (c) Find the dimensions of the rectangle.

Answer 1

Answer: (a)
`A = x^(2)-7x`

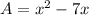
(b) x = 12 or x = -5

(c) Length = 12cm

Width = 5cm

Explanation: Area of a rectangle is calculated as:

A = length*width

(a) If length = x,

width = x - 7

Then, equation is:

A = x(x - 7)

`A = x^(2) - 7x`

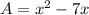
(b) Solving for x:

`A = x^(2) - 7x`

`x^(2) - 7x = 60`

`x^(2) - 7x - 60=0`

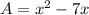
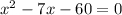
Using Bhaskara to solve equation:

`x = \frac{7+\sqrt{(-7)^(2)-4.1.(-60)} }{2}`

`x =(7+√(289) )/(2)`

`x =(7+17)/(2)`

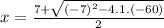
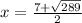
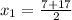`x_(1) = (7+17)/(2)` = 12

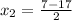`x_(2)=(7-17)/(2)` = -5

The quadratic equation gives two values for x: x = 12 or x = -5

(c) Dimensions are positive numbers, so the value of x used is x = 12.

As length is x:

length = 12cm

Width is 7 less than length:

width = x - 7

width = 5cm

The rectangle has length of 12cm and width of 5cm.