Question

. Leah invested some money at 4.5% annual interest and $1000 more than four times that amount at 6%. Her total annual income from these two investments was $801. How much did she invest at each rate

Answer 1

The amount invested are $2600 and $11400 respectively

Explanation:

Let the first amount be x

Given:

(First Investment)

Principal (P1) = x

Rate (R1) = 4.5%

Time (T) = 1 year

(Second Investment)

Principal (P2) = 4x + 1000

Rate (R2) = 6%

Time (T) = 1 year

Income = $801

Calculating the income from the first investment;

`I_1 = (P_1R_1T)/(100)`

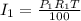
Substitute values for P1, R1 and T

`I_1 = (x * 4.5 * 1)/(100)`

`I_1 = (4.5x)/(100)`

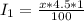
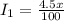
Calculating the income from the second investment;

`I_2 = (P_2R_2T)/(100)`

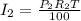
Substitute values for P2, R2 and T

`I_2 = ((4x + 1000) * 6 * 1)/(100)`

`I_2 = (6(4x + 1000))/(100)`

`I_1 + I_2 = Annual\ Income`

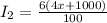
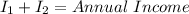
So:

`(4.5x)/(100) + (6(4x + 1000))/(100) = 801`

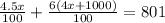
Multiply through by 100

`100 * (4.5x)/(100) +100 * (6(4x + 1000))/(100) = 801 * 100`

`4.5x +6(4x + 1000) = 801 * 100`

`4.5x +24x + 6000 = 80100`

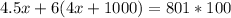
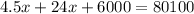
Collect Like Terms

`4.5x +24x = 80100 - 6000`

`28.5x = 74100`

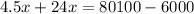
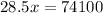
Divide through by 28.5

`x = (74100)/(28.5)`

`x = \$2600`

Recall that; the second invest

Amount Invested = 4x + 1000

This gives

`Amount = 4 * \$2600 + 1000`

`Amount = \$11400`

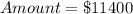
Hence;

The amount invested are $2600 and $11400 respectively