Answer:
The answer is
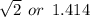
Explanation:
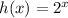
To solve the equation we must first find h-¹(x)
To find h-¹(x) equate h(x) to y
That's
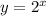
Next interchange the terms
x becomes y and y becomes x
That's
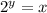
Make y the subject
Take logarithm to base 2 to both sides
That's
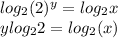
But

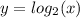
So we have
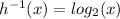
Now we can solve the equation
We have

Convert the logarithm into exponential form using the fact that
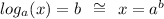
So we have

But
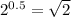
So we have the final answer as
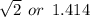
Hope this helps you