Answer:
A)
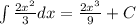
B)
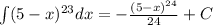
Explanation:
A)
So we have the integral:
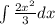
First, remove the constant multiple:
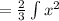
Use the power rule, where:
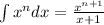
Therefore:
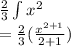
Simplify:
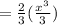
And multiply:
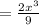
And, finally, plus C:
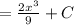
B)
We have the integral:
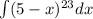
To solve, we can use u-substitute.
Let u equal 5-x. Then:
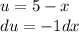
So:
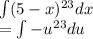
Move the negative outside:
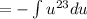
Power rule:
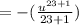
Add:
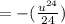
Substitute back 5-x:
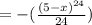
Constant of integration:
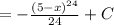
And we're done!