Question

Find all x-intercepts and y-intercepts of the graph of the function . f(x) = - x ^ 3 + x ^ 2 + 12x If there is more than one answer, separate them with commas. Click on "None" if applicable.

Answer 1

The y-intercept is (0,0)

The x-intercepts are (-3,0), (0,0), and (4,0)

Explanation:

So we have the function:

`f(x)=-x^3+x^2+12x`

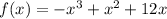
And we want to solve for the x- and y-intercepts.

Y)

To solve for the y-intercept, recall that the y-intercept is when the graph touches the y-axis. At that point, the x values is 0. Thus, to find the x-intercept, substitute 0 for x:

`f(x)=-(0)^3+(0)^2+12(0)`

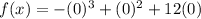
Simplify:

`f(x)=0`

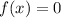
So, the y-intercept is (0,0)

X)

To solve for the x-intercept(s), set the function equal to 0 and solve for x:

`0=-x^3+x^2+12x`

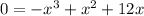
First, factor out a negative x:

`0=-x(x^2-x-12)`

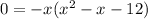
Factor within the parentheses:

`0=-x(x-4)(x+3)`

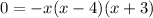
Zero Product Property:

`-x=0\text{ or } x-4=0\text{ or } x+3=0`

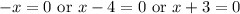
Divide by -1 on the first one. Add 4 on the second one. And subtract 3 on the right:

`x=0\text{ or } x=4\text{ or } x=-3`

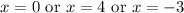
So, our x-intercepts are:

`(-3,0), (0,0), (4,0)`

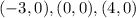
And we're done :)