Question

Write the equation of the parabola in vertex form vertex (0,0) passes through (2,1)

Answer 1

`f(x)=(1)/(4)x^2`

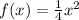
Explanation:

Recall the vertex form of a quadratic equation:

`f(x)=a(x-h)^2+k`

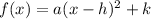
Where (h,k) is the vertex.

We are told that the vertex is (0,0). Therefore:

`f(x)=a(x-0)^2+(0)`

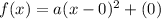
Simplify:

`f(x)=ax^2`

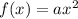
So, to finish the equation, we need to find a.

We know that a point is (2,1). Thus, substitute 1 for f(x) and 2 for x:

`1=a(2)^2`

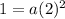
Square:

`1=4a`

Divide both sides by 4:

`a=(1)/(4)`

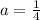
So, our a value is 1/4.

And we can thus complete our equation:

`f(x)=(1)/(4)x^2`

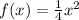
And we are done :)